1371. Быстрые ответы
Джо любит
компьютерные игры. Сейчас он должен решить головоломку. Перед ним лежит
огромная карта с укрепленными городами. Враг Джо – очень сильный и хитрый
персонаж, который умеет соединять и разъединять города своими командами. Два города
называются связанными, если они соединены либо непосредственно, либо через
некоторое множество других связанных между собой городов в некоторый момент
времени. Когда город отключается, он становится изолированным от других, то
есть удаляется вся история его соединений; история соединений между другими
городами не изменяется. Каждое соединение является двунаправленным. Изначально
все города изолированы. Джо необходимо быстро отвечать, связаны ли два города,
в соответствии с историей команд персонажа.
Напишите
программу, которая на основе входных данных подсчитает количество ответов “да” и количество
ответов “нет” на вопросы следующего вида: связаны ли между собой города towni и townj?
Вход. Состоит из нескольких тестов, каждый из которых
представляет собой отдельную карту городов и команд персонажа:
1) Количество городов на карте n (n ≤ 10000);
2) Набор команд вида:
a) c towni
townj, где towni и townj – целые числа от 1 до no_of_towns. Команда означает, что towni и townj
соединяются.
b) d towni, где towni – целое число от 1 до no_of_towns. Команда означает, что towni отсоединяется.
c) q towni townj, где
towni и townj – целые числа от 1 до no_of_towns. Команда означает запрос:
соединены ли towni с townj?
d) e, завершающая список команд.
Каждая команда расположена в отдельной строке. Команды (a),
(b), (c) могут идти в любом порядке. Связность городов изменяется при
поступлении команд типа (a) и (b). Каждая команда типа (c) обрабатывается в
соответствии с текущей конфигурацией.
Выход. Вывести найденные два числа в одной строке в
виде: n1, n2, как показано в
примере.
Пример. Приведенный пример соответствует карте
из 4 укрепленных городов. Персонаж дает 9 команд. Имеется в точности n1 ответов yes и n2 ответов no.
|
Пример
входа |
Пример
выхода |
|
4 c 1 2 c 3 4 q 1 3 c 2 3 q 1 4 d 2 q 4 1 q 2 4 e |
2 , 2 |
РЕШЕНИЕ
структуры
данных - система непересекающихся множеств
Анализ алгоритма
Введем понятие идентификационного кода города. Изначально
положим Id[i] = i. При обработке запросов типа c
и q на системе непересекающихся
множеств будем обрабатывать ячейки массивов, которые соответствуют
идентификационным кодам городов. Пусть MaxID содержит минимальный еще неиспользованный
код города (изначально имеется n
городов, положим MaxID = n + 1). Тогда отсоединение города (запрос
типа d towni) реализуем тем, что городу towni назначим новый id
код (например Id[i] = MaxID++). Таким образом старые связи
(память у городов) остаются, а новый город реально становится отсоединенным от
остальных.
Например, для объединения городов i и j будет вызвана функция
Union(Id[i], Id[j]).
Представитель города i возвращается функцией Repr(Id[i]).
Пример
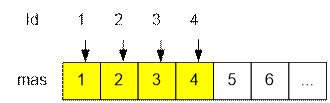
Инициализируем массив mas и массив идентификационных кодов. Идентификационный код каждого города изначально равен
номеру самого города (Id[i] = i).
Обработаем первые три запроса. В двух запросах производится
соединение городов 1 и 2, 3 и 4. Граф принимает вид:

Ответом на запрос q(1,
3) будет no,
так как вершины 1 и 3 несвязны.
Следующим запросом происходит объединение городов 2 и 3.
Вершины 1 и 4 становятся связными. Запрос q(1,
4) дает
ответ yes.

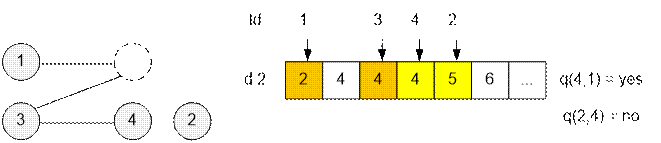
Следующим запросом (d
2) отсоединяется город 2. Городу 2 присваиваем новый id код. Минимальным еще неиспользованным
кодом города является 5. Положим Id[2] = 5. Города 4 и 1 являются
связными (связь не разорвалась). Города 2 и 4 не связаны друг с другом.
Например, для запроса q(2, 4) следует проверить, равны ли Repr(Id[2]) и Repr(Id[4]) (или Repr(5) и Repr(4)). Учитывая что Repr(5) = 5, Repr(4) = 4, заключаем
что вершины 2 и 4 несвязны.
Реализация алгоритма
Объявим массив
mas, используемый системой непересекающихся множеств. А также массив Id, содержащий
текущие идентификационные коды городов.
#define MAX 100010
int mas[MAX], Id[MAX];
Функция Repr возвращает
представителя множества, которому принадлежит вершина n.
int Repr(int
n)
{
if (n ==
mas[n]) return n;
return mas[n]
= Repr(mas[n]);
}
Функция Union объединяет множества, которым
принадлежат вершины x и y.
int Union(int
x,int y)
{
int x1 =
Repr(x),y1 = Repr(y);
mas[x1] = y1;
return (x1 !=
y1);
}
Основная часть программы.
while(scanf("%d\n",&n)
== 1)
{
Инициализация массивов и переменных.
for(i = 1; i
< MAX; i++) mas[i] = i, Id[i] = i;
MaxID = n + 1;
n1 = n2 = 0;
Последовательно обрабатываем запросы.
while(scanf("%c",&c), c != 'e')
{
Объединение городов towni и townj.
if (c == 'c')
{
scanf("%d
%d\n",&i,&j);
Union(Id[i],Id[j]);
}
Отсоединение города towni.
if (c == 'd')
{
scanf("%d\n",&i);
Id[i] = MaxID++;
}
Проверяем, соединены ли towni с townj.
if (c == 'q')
{
scanf("%d
%d\n",&i,&j);
if
(Repr(Id[i]) == Repr(Id[j])) n1++; else n2++;
}
}
Выводим ответ.
printf("%d ,
%d\n",n1,n2);
}